Regression Analysis

This example uses the ‘diabetes’ data from sklearn datasets and performs a regression analysis using a Ridge Regression model.

# Authors: Shammi More <s.more@fz-juelich.de>
#          Federico Raimondo <f.raimondo@fz-juelich.de>
#
# License: AGPL

import pandas as pd
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_diabetes
from sklearn.metrics import mean_absolute_error
from sklearn.model_selection import train_test_split

from julearn import run_cross_validation
from julearn.utils import configure_logging

Set the logging level to info to see extra information

configure_logging(level='INFO')

2023-04-06 09:51:12,669 - julearn - INFO - ===== Lib Versions =====
2023-04-06 09:51:12,670 - julearn - INFO - numpy: 1.23.5
2023-04-06 09:51:12,670 - julearn - INFO - scipy: 1.10.1
2023-04-06 09:51:12,670 - julearn - INFO - sklearn: 1.0.2
2023-04-06 09:51:12,670 - julearn - INFO - pandas: 1.4.4
2023-04-06 09:51:12,670 - julearn - INFO - julearn: 0.3.1.dev2
2023-04-06 09:51:12,670 - julearn - INFO - ========================

load the diabetes data from sklearn as a pandas dataframe

features, target = load_diabetes(return_X_y=True, as_frame=True)

Dataset contains ten variables age, sex, body mass index, average blood pressure, and six blood serum measurements (s1-s6) diabetes patients and a quantitative measure of disease progression one year after baseline which is the target we are interested in predicting.

print('Features: \n', features.head())
print('Target: \n', target.describe())

Features:
         age       sex       bmi  ...        s4        s5        s6
0  0.038076  0.050680  0.061696  ... -0.002592  0.019908 -0.017646
1 -0.001882 -0.044642 -0.051474  ... -0.039493 -0.068330 -0.092204
2  0.085299  0.050680  0.044451  ... -0.002592  0.002864 -0.025930
3 -0.089063 -0.044642 -0.011595  ...  0.034309  0.022692 -0.009362
4  0.005383 -0.044642 -0.036385  ... -0.002592 -0.031991 -0.046641

[5 rows x 10 columns]
Target:
 count    442.000000
mean     152.133484
std       77.093005
min       25.000000
25%       87.000000
50%      140.500000
75%      211.500000
max      346.000000
Name: target, dtype: float64

Let’s combine features and target together in one dataframe and define X and y

data_diabetes = pd.concat([features, target], axis=1)

X = ['age', 'sex', 'bmi', 'bp', 's1', 's2', 's3', 's4', 's5', 's6']
y = 'target'

calculate correlations between the features/variables and plot it as heat map

corr = data_diabetes.corr()
fig, ax = plt.subplots(1, 1, figsize=(10, 7))
sns.set(font_scale=1.2)
sns.heatmap(corr, xticklabels=corr.columns, yticklabels=corr.columns,
            annot=True, fmt="0.1f")

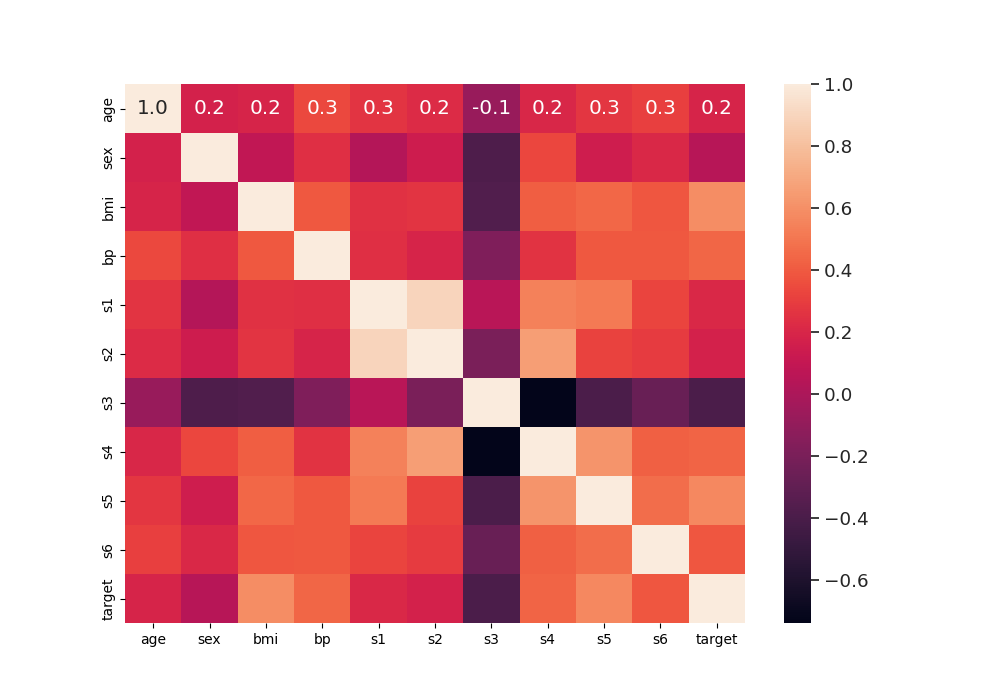
<Axes: >

Split the dataset into train and test

train_diabetes, test_diabetes = train_test_split(data_diabetes, test_size=0.3)

Train a ridge regression model on train dataset and use mean absolute error for scoring

scores, model = run_cross_validation(
    X=X, y=y, data=train_diabetes, preprocess_X='zscore',
    problem_type='regression', model='ridge', return_estimator='final',
    scoring='neg_mean_absolute_error')

2023-04-06 09:51:13,121 - julearn - INFO - Using default CV
2023-04-06 09:51:13,121 - julearn - INFO - ==== Input Data ====
2023-04-06 09:51:13,121 - julearn - INFO - Using dataframe as input
2023-04-06 09:51:13,121 - julearn - INFO - Features: ['age', 'sex', 'bmi', 'bp', 's1', 's2', 's3', 's4', 's5', 's6']
2023-04-06 09:51:13,121 - julearn - INFO - Target: target
2023-04-06 09:51:13,122 - julearn - INFO - Expanded X: ['age', 'sex', 'bmi', 'bp', 's1', 's2', 's3', 's4', 's5', 's6']
2023-04-06 09:51:13,122 - julearn - INFO - Expanded Confounds: []
2023-04-06 09:51:13,123 - julearn - INFO - ====================
2023-04-06 09:51:13,123 - julearn - INFO -
2023-04-06 09:51:13,123 - julearn - INFO - ====== Model ======
2023-04-06 09:51:13,123 - julearn - INFO - Obtaining model by name: ridge
2023-04-06 09:51:13,123 - julearn - INFO - ===================
2023-04-06 09:51:13,123 - julearn - INFO -
2023-04-06 09:51:13,124 - julearn - INFO - CV interpreted as RepeatedKFold with 5 repetitions of 5 folds

The scores dataframe has all the values for each CV split.

print(scores.head())

   fit_time  score_time  test_score  repeat  fold
0  0.013107    0.008715  -43.906430       0     0
1  0.013143    0.009089  -44.127262       0     1
2  0.013696    0.008770  -45.136034       0     2
3  0.013036    0.008527  -41.324288       0     3
4  0.012734    0.008869  -47.367616       0     4

Mean value of mean absolute error across CV

print(scores['test_score'].mean() * -1)

43.98214011826165

Now we can get the MAE fold and repetition:

df_mae = scores.set_index(
    ['repeat', 'fold'])['test_score'].unstack() * -1
df_mae.index.name = 'Repeats'
df_mae.columns.name = 'K-fold splits'

print(df_mae)

K-fold splits          0          1          2          3          4
Repeats
0              43.906430  44.127262  45.136034  41.324288  47.367616
1              43.647265  43.816622  44.047904  45.788798  41.244561
2              49.546995  43.503900  43.895329  38.566435  45.413806
3              45.911183  43.881612  47.925275  42.304993  39.137493
4              49.955405  35.486691  46.914710  43.613901  43.088996

Plot heatmap of mean absolute error (MAE) over all repeats and CV splits

fig, ax = plt.subplots(1, 1, figsize=(10, 7))
sns.heatmap(df_mae, cmap="YlGnBu")
plt.title('Cross-validation MAE')

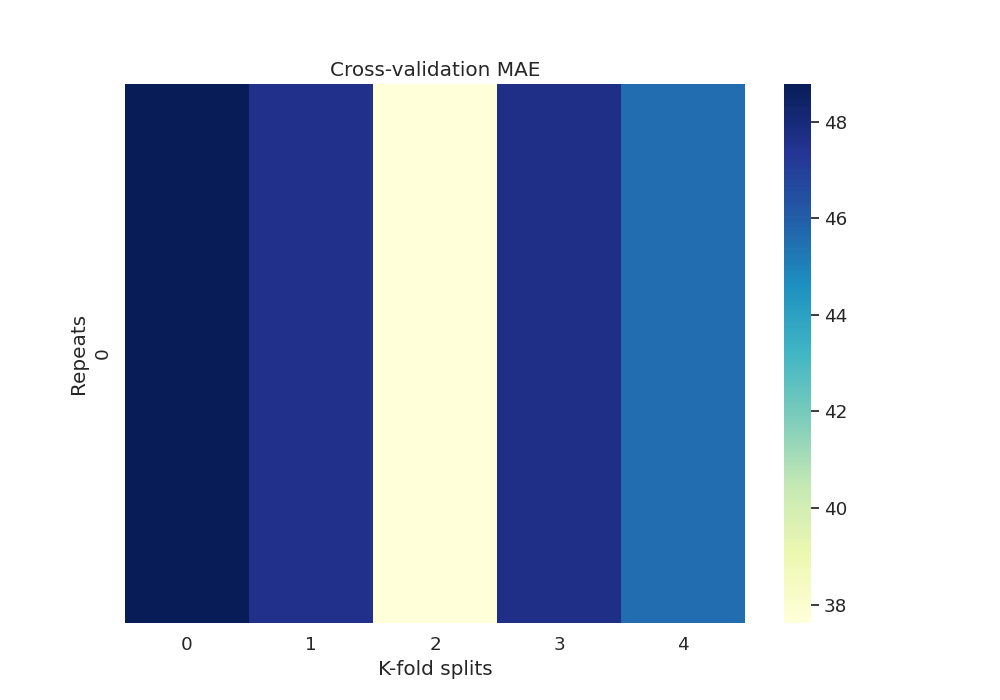
Text(0.5, 1.0, 'Cross-validation MAE')

Let’s plot the feature importance using the coefficients of the trained model

features = pd.DataFrame({'Features': X, 'importance': model['ridge'].coef_})
features.sort_values(by=['importance'], ascending=True, inplace=True)
features['positive'] = features['importance'] > 0

fig, ax = plt.subplots(1, 1, figsize=(10, 7))
features.set_index('Features', inplace=True)
features.importance.plot(kind='barh',
                         color=features.positive.map
                         ({True: 'blue', False: 'red'}))
ax.set(xlabel='Importance', title='Variable importance for Ridge Regression')

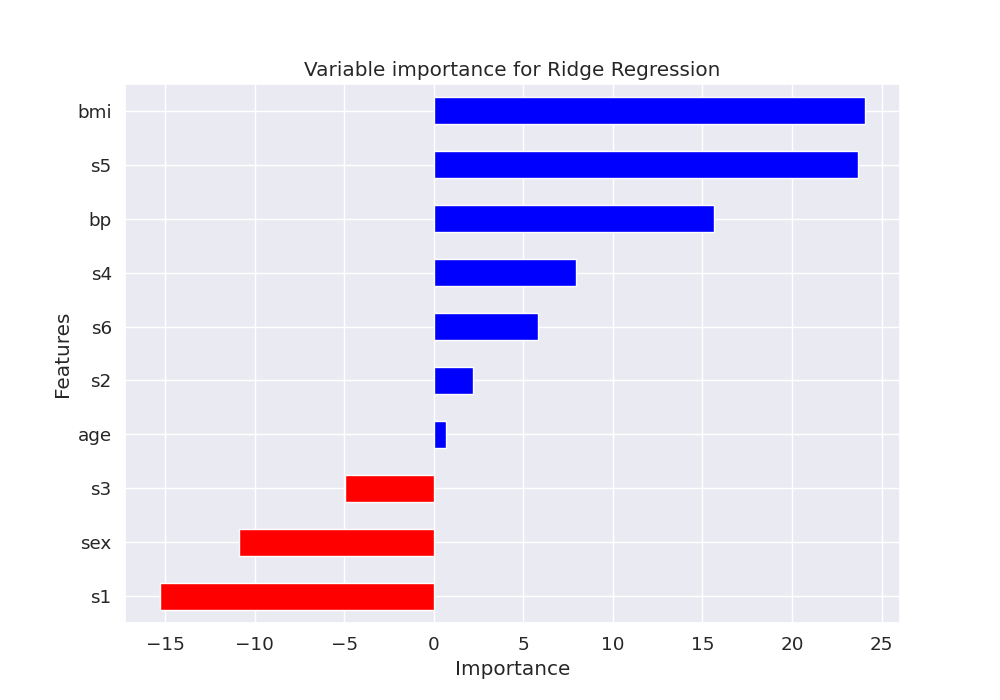
[Text(0.5, 40.249999999999986, 'Importance'), Text(0.5, 1.0, 'Variable importance for Ridge Regression')]

Use the final model to make predictions on test data and plot scatterplot of true values vs predicted values

y_true = test_diabetes[y]
y_pred = model.predict(test_diabetes[X])
mae = format(mean_absolute_error(y_true, y_pred), '.2f')
corr = format(np.corrcoef(y_pred, y_true)[1, 0], '.2f')

fig, ax = plt.subplots(1, 1, figsize=(10, 7))
sns.set_style("darkgrid")
plt.scatter(y_true, y_pred)
plt.plot(y_true, y_true)
xmin, xmax = ax.get_xlim()
ymin, ymax = ax.get_ylim()
text = 'MAE: ' + str(mae) + '   CORR: ' + str(corr)
ax.set(xlabel='True values', ylabel='Predicted values')
plt.title('Actual vs Predicted')
plt.text(xmax - 0.01 * xmax, ymax - 0.01 * ymax, text, verticalalignment='top',
         horizontalalignment='right', fontsize=12)
plt.axis('scaled')

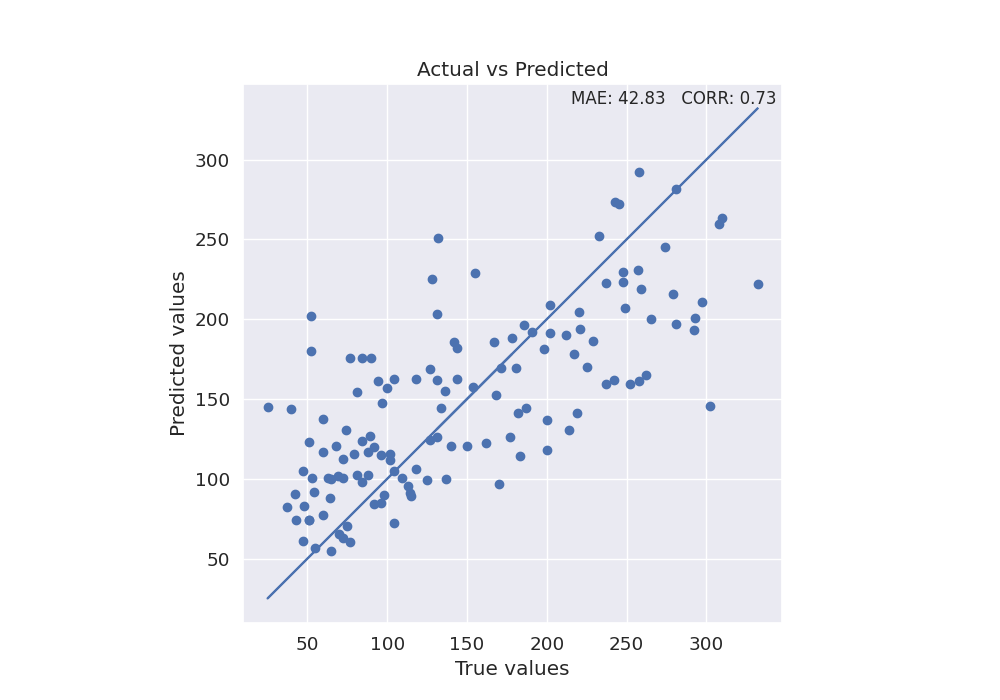
(9.45, 351.55, 9.45, 351.55)