Confound Removal (model comparison)

This example uses the ‘iris’ dataset, performs simple binary classification with and without confound removal using a Random Forest classifier.

# Authors: Shammi More <s.more@fz-juelich.de>
#          Federico Raimondo <f.raimondo@fz-juelich.de>
#
# License: AGPL

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from seaborn import load_dataset

from julearn import run_cross_validation
from julearn.utils import configure_logging
from julearn.model_selection import StratifiedBootstrap

Set the logging level to info to see extra information

configure_logging(level='INFO')

2023-04-06 09:51:14,586 - julearn - INFO - ===== Lib Versions =====
2023-04-06 09:51:14,586 - julearn - INFO - numpy: 1.23.5
2023-04-06 09:51:14,586 - julearn - INFO - scipy: 1.10.1
2023-04-06 09:51:14,586 - julearn - INFO - sklearn: 1.0.2
2023-04-06 09:51:14,586 - julearn - INFO - pandas: 1.4.4
2023-04-06 09:51:14,586 - julearn - INFO - julearn: 0.3.1.dev2
2023-04-06 09:51:14,586 - julearn - INFO - ========================

load the iris data from seaborn

df_iris = load_dataset('iris')

The dataset has three kind of species. We will keep two to perform a binary classification.

df_iris = df_iris[df_iris['species'].isin(['versicolor', 'virginica'])]

As features, we will use the sepal length, width and petal length and use petal width as confound.

X = ['sepal_length', 'sepal_width', 'petal_length']
y = 'species'
confound = 'petal_width'

Doing hypothesis testing in ML is not that simple. If we were to used classical frequentist statistics, we have the problem that using cross validation, the samples are not independent and the population (train + test) is always the same.

If we want to compare two models, an alternative is to contrast, for each fold, the performance gap between the models. If we combine that approach with bootstrapping, we can then compare the confidence intervals of the difference. If the 95% CI is above 0 (or below), we can claim that the models are different with p < 0.05.

Lets use a bootstrap CV. For time purposes we do 20 iterations, change the number of bootstrap iterations to at least 2000 for a valid test.

n_bootstrap = 20
n_elements = len(df_iris)
cv = StratifiedBootstrap(n_splits=n_bootstrap, test_size=.3, random_state=42)

First, we will train a model without performing confound removal on features Note: confounds=None by default

scores_ncr = run_cross_validation(
    X=X, y=y, data=df_iris, model='rf', cv=cv, preprocess_X='zscore',
    scoring=['accuracy', 'roc_auc'], return_estimator='cv', seed=200)

2023-04-06 09:51:14,591 - julearn - INFO - Setting random seed to 200
2023-04-06 09:51:14,591 - julearn - INFO - ==== Input Data ====
2023-04-06 09:51:14,591 - julearn - INFO - Using dataframe as input
2023-04-06 09:51:14,591 - julearn - INFO - Features: ['sepal_length', 'sepal_width', 'petal_length']
2023-04-06 09:51:14,592 - julearn - INFO - Target: species
2023-04-06 09:51:14,592 - julearn - INFO - Expanded X: ['sepal_length', 'sepal_width', 'petal_length']
2023-04-06 09:51:14,592 - julearn - INFO - Expanded Confounds: []
2023-04-06 09:51:14,593 - julearn - INFO - ====================
2023-04-06 09:51:14,593 - julearn - INFO -
2023-04-06 09:51:14,593 - julearn - INFO - ====== Model ======
2023-04-06 09:51:14,593 - julearn - INFO - Obtaining model by name: rf
2023-04-06 09:51:14,593 - julearn - INFO - ===================
2023-04-06 09:51:14,593 - julearn - INFO -
2023-04-06 09:51:14,594 - julearn - INFO - Using scikit-learn CV scheme StratifiedBootstrap(n_splits=20, random_state=42, test_size=0.3,
          train_size=None)

Next, we train a model after performing confound removal on the features Note: we initialize the CV again to use the same folds as before

cv = StratifiedBootstrap(n_splits=n_bootstrap, test_size=.3, random_state=42)
scores_cr = run_cross_validation(
    X=X, y=y, confounds=confound, data=df_iris, model='rf',
    preprocess_X='remove_confound', preprocess_confounds='zscore', cv=cv,
    scoring=['accuracy', 'roc_auc'], return_estimator='cv', seed=200)

2023-04-06 09:51:18,895 - julearn - INFO - Setting random seed to 200
2023-04-06 09:51:18,895 - julearn - INFO - ==== Input Data ====
2023-04-06 09:51:18,895 - julearn - INFO - Using dataframe as input
2023-04-06 09:51:18,895 - julearn - INFO - Features: ['sepal_length', 'sepal_width', 'petal_length']
2023-04-06 09:51:18,895 - julearn - INFO - Target: species
2023-04-06 09:51:18,895 - julearn - INFO - Confounds: petal_width
2023-04-06 09:51:18,896 - julearn - INFO - Expanded X: ['sepal_length', 'sepal_width', 'petal_length']
2023-04-06 09:51:18,896 - julearn - INFO - Expanded Confounds: ['petal_width']
2023-04-06 09:51:18,896 - julearn - INFO - ====================
2023-04-06 09:51:18,897 - julearn - INFO -
2023-04-06 09:51:18,897 - julearn - INFO - ====== Model ======
2023-04-06 09:51:18,897 - julearn - INFO - Obtaining model by name: rf
2023-04-06 09:51:18,897 - julearn - INFO - ===================
2023-04-06 09:51:18,897 - julearn - INFO -
2023-04-06 09:51:18,898 - julearn - INFO - Using scikit-learn CV scheme StratifiedBootstrap(n_splits=20, random_state=42, test_size=0.3,
          train_size=None)

Now we can compare the accuracies. We can combine the two outputs as pandas dataframes

scores_ncr['confounds'] = 'Not Removed'
scores_cr['confounds'] = 'Removed'

Now we convert the metrics to a column for easier seaborn plotting (convert to long format)

index = ['fold', 'confounds']
scorings = ['test_accuracy', 'test_roc_auc']

df_ncr_metrics = scores_ncr.set_index(index)[scorings].stack()
df_ncr_metrics.index.names = ['fold', 'confounds', 'metric']
df_ncr_metrics.name = 'value'

df_cr_metrics = scores_cr.set_index(index)[scorings].stack()
df_cr_metrics.index.names = ['fold', 'confounds', 'metric']
df_cr_metrics.name = 'value'

df_metrics = pd.concat((df_ncr_metrics, df_cr_metrics))

df_metrics = df_metrics.reset_index()
print(df_metrics.head())

   fold    confounds         metric     value
0     0  Not Removed  test_accuracy  0.933333
1     0  Not Removed   test_roc_auc  0.968889
2     1  Not Removed  test_accuracy  0.933333
3     1  Not Removed   test_roc_auc  0.948889
4     2  Not Removed  test_accuracy  1.000000

And finally plot the results

sns.catplot(x='confounds', y='value', col='metric', data=df_metrics,
            kind='swarm')
plt.tight_layout()

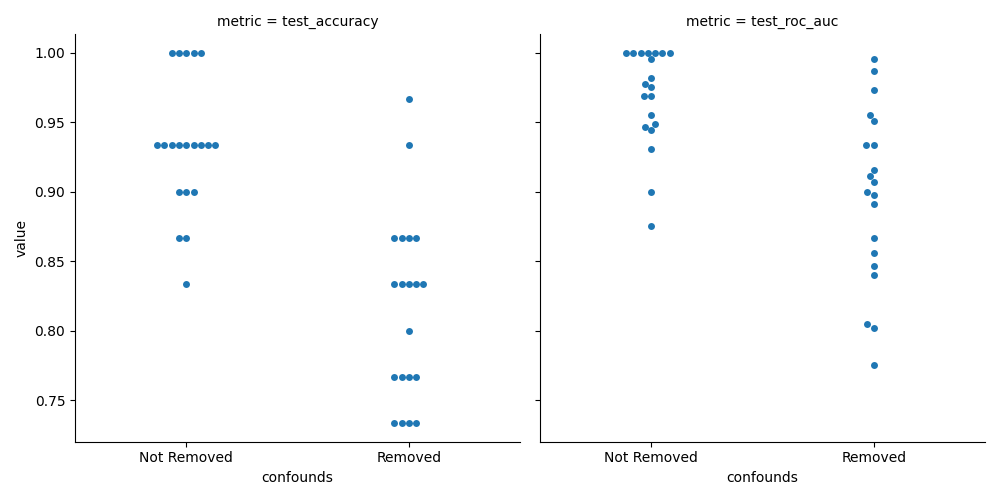
While this plot allows us to see the mean performance values and compare them, these samples are paired. In order to see if there is a systematic difference, we need to check the distribution of differeces between the the models.

First we remove the column “confounds” from the index and make the difference between the metrics

df_cr_metrics = df_cr_metrics.reset_index().set_index(['fold', 'metric'])
df_ncr_metrics = df_ncr_metrics.reset_index().set_index(['fold', 'metric'])

df_diff_metrics = df_ncr_metrics['value'] - df_cr_metrics['value']
df_diff_metrics = df_diff_metrics.reset_index()

Now we can finally plot the difference, setting the whiskers of the box plot at 2.5 and 97.5 to see the 95% CI.

sns.boxplot(x='metric', y='value', data=df_diff_metrics.reset_index(),
            whis=[2.5, 97.5])
plt.axhline(0, color='k', ls=':')
plt.tight_layout()

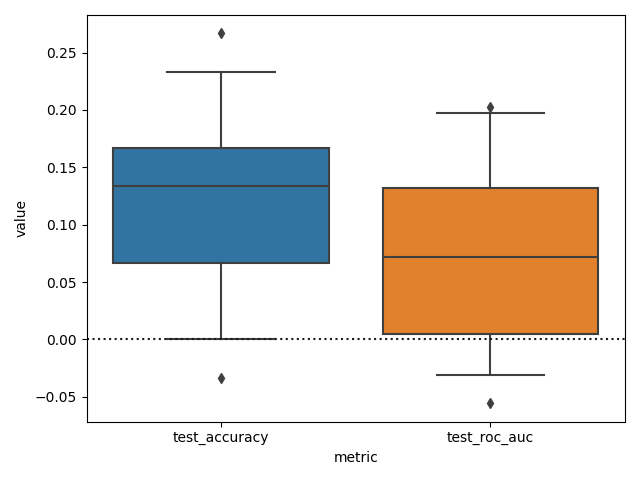
We can see that while it seems that the accuracy and ROC AUC scores are higher when confounds are not removed. We can not really claim (using this test), that the models are different in terms of these metrics.

Maybe the percentiles will be more accuracy with the proper amount of bootstrap iterations?

But the main point of confound removal is for interpretability. Lets see if there is a change in the feature importances.

First, we need to collect the feature importances for each model, for each fold.

ncr_fi = []
for i_fold, estimator in enumerate(scores_ncr['estimator']):
    this_importances = pd.DataFrame({
        'feature': [x.replace('_', ' ') for x in X],
        'importance': estimator['rf'].feature_importances_,
        'confounds': 'Not Removed',
        'fold': i_fold
    })
    ncr_fi.append(this_importances)
ncr_fi = pd.concat(ncr_fi)

cr_fi = []
for i_fold, estimator in enumerate(scores_cr['estimator']):
    this_importances = pd.DataFrame({
        'feature': [x.replace('_', ' ') for x in X],
        'importance': estimator['rf'].feature_importances_,
        'confounds': 'Removed',
        'fold': i_fold
    })
    cr_fi.append(this_importances)
cr_fi = pd.concat(cr_fi)

feature_importance = pd.concat([cr_fi, ncr_fi])

We can now plot the importances

sns.catplot(x='feature', y='importance', hue='confounds', dodge=True,
            data=feature_importance, kind='swarm', s=3)
plt.tight_layout()

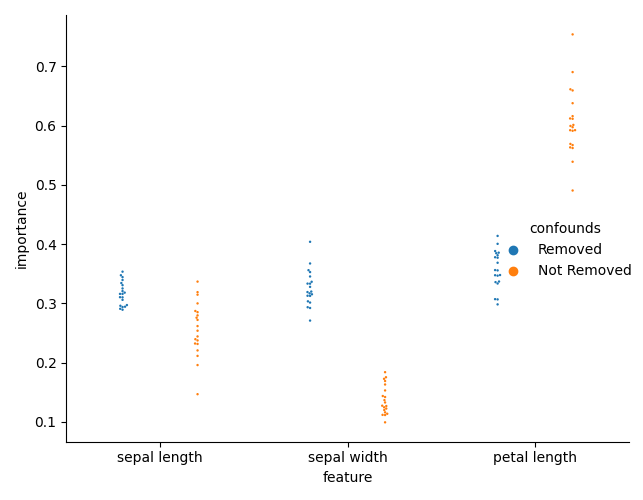
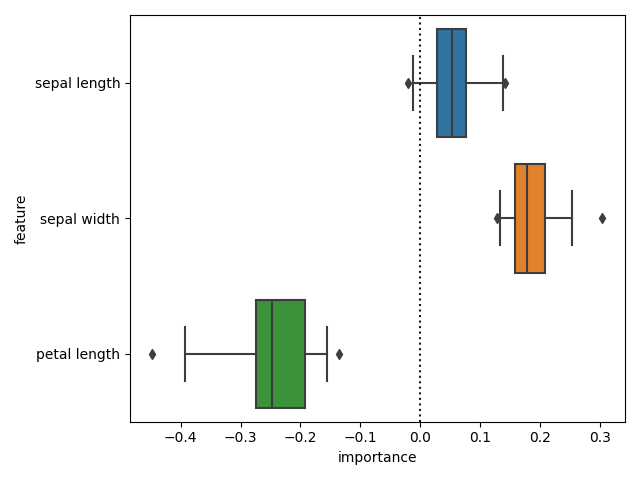
And check the differences in importances. We can now see that there is a difference in importances.

diff_fi = (cr_fi.set_index(['feature', 'fold'])['importance'] -
           ncr_fi.set_index(['feature', 'fold'])['importance'])
sns.boxplot(x='importance', y='feature', data=diff_fi.reset_index(),
            whis=[2.5, 97.5])
plt.axvline(0, color='k', ls=':')
plt.tight_layout()